La Gran Pirámide y el espacio
LA GRAN PIRÁMIDE DE KEOPS [Khufu]
El codo real y el metro
La relación entre el codo real y el metro ha sido establecida por los estudios egiptológicos realizados hasta ahora, que se han basado en la medida de varas de madera con marcas en codos reales. El resultado obtenido es 1 codo real = 0,5236 m.
Al respecto, se produce un hecho desconcertante: 0,5236 equivale, a la vez, a Π / 6 y a Φ2 / 5, ya que 3,1416 / 6 = 0,5236, y también, 2,6180 / 5 = 0,5236.
El Número Π dividido por 6 es igual al cuadrado del Número de Oro dividido por 5. El resultado es 0,5236.
Y 1 codo real era igual a… ¡0,5236 metros!
En una circunferencia de 1 metro de diámetro, el arco de circunferencia que corresponde a un lado de un hexágono inscrito es igual a 1 codo real. (fig. 16)
El resultado es muy desconcertante porque presupone lo siguiente:
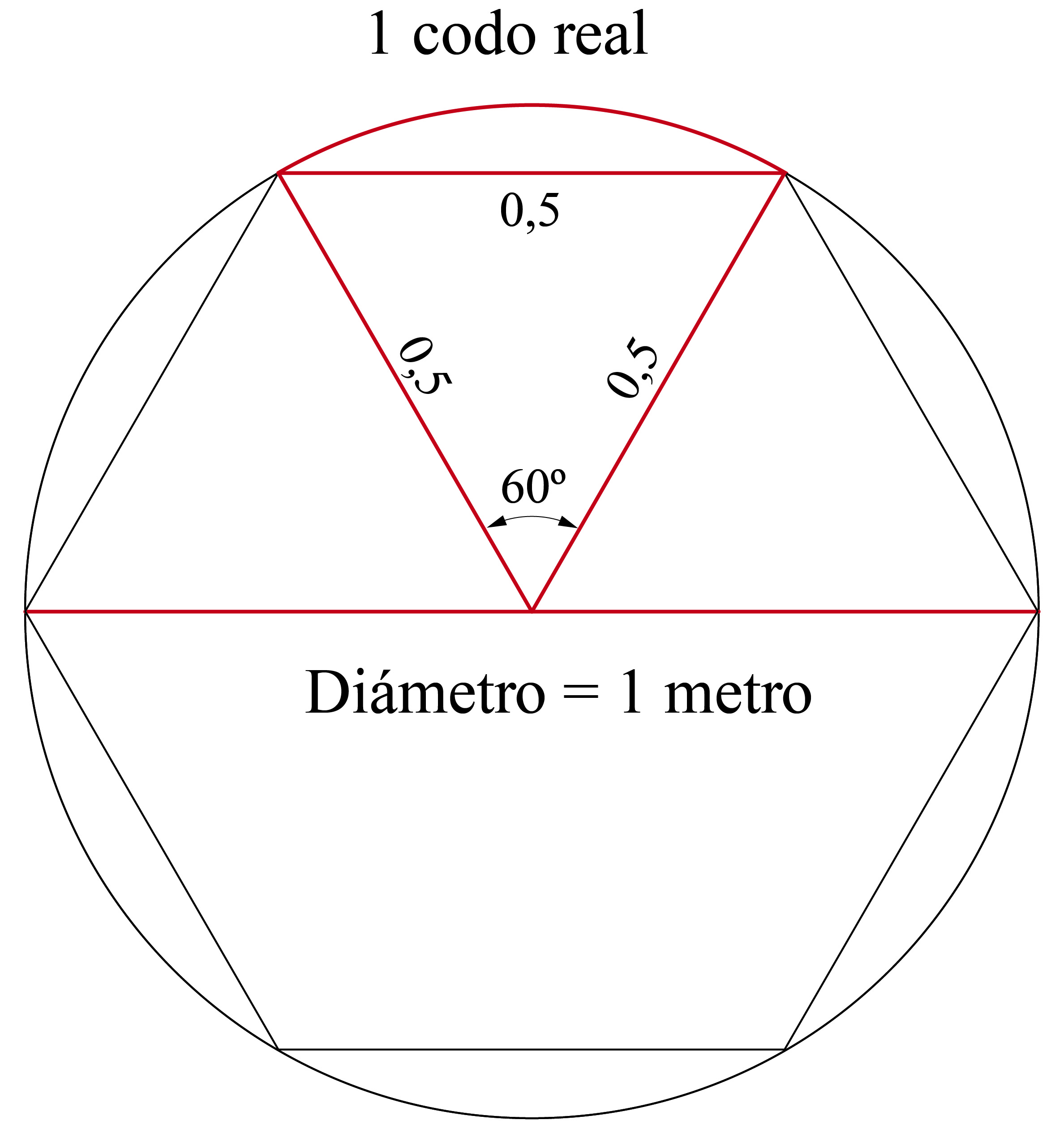
Figura 16. La relación geométrica entre el codo real y el metro.
¿El metro en la Gran Pirámide?
Una vez reconstruido el modelo de la Gran Pirámide, se realizó un minucioso análisis de sus medidas. Y uno de los resultados más excepcionales obtenidos fue la longitud de la arista. Esta longitud que era especialmente significativa porque elevaba el monumento hacia el cielo.
Es decir, parecía como si la Gran Pirámide hubiera sido diseñada, a la vez, en codos reales y en metros. Porque las dos principales longitudes que definían su forma, se expresaban en números enteros: el lado de la base medía 440 codos reales y la arista, 218 metros.
¿Se podía tratar de una casualidad?
El análisis de las medidas de la Cámara del Rey, que se mantiene intacta en el interior del monumento, insistía triplemente en la presencia de medidas exactas en metros:
- La altura sobre el zócalo [1] es de 43,00 m.
- La diagonal del muro mayor de la Cámara del Rey mide 12,00 m.
- Su volumen es de 321,00 m3.
Por si no fuese suficiente, la suma de la base (440 cr) y la altura (280 cr) de la Gran Pirámide es igual a 720 cr, una medida que coincide exactamente con 377,00 m. Y como hemos visto, da la casualidad que el 377 es el 14.º número de la Serie de Fibonacci.
Ante la insistencia de tantas medidas en metros, es obligado que nos preguntemos:
Para intentar responder a esta pregunta, veamos si las medidas en metros nos proponen juegos numéricos.
Sumemos las 9 longitudes obtenidas: las 4 aristas (4 x 218 = 872 m), más las 4 diagonales de los muros mayores de la Cámara del Rey (4 x 12 = 48 m), más su altura sobre el zócalo (43 m). Resultará 963 m. Y, curiosamente, esta cifra es el triple de 321, el número que expresa el volumen de la Cámara del Rey en m3.
¿Se trata de otra casualidad?
Figura 17. A la izquierda la Gran Galería. A la derecha, La Cámara del Rey de la Gran Pirámide.
Al llegar a este punto, como había números que establecían juegos entre ellos o se repetían insistentemente en la Gran Pirámide, recordé que Pitágoras [2] estudió en Egipto, donde vivió entre 10 y 20 años, y donde fue ungido sacerdote, por lo que tuvo acceso a sus conocimientos. Por eso no es extraño que el llamado Teorema de Pitágoras se halle en la Gran Pirámide.
Pitágoras y los pitagóricos afirmaban que “todo es número”, por lo que consideraban a los números como divinidades o como entidades abstractas preexistentes e independientes de su unidad de medida.
Este hecho viene confirmado por nuestra cotidiana práctica mental. Si un amigo con el que estás hablando, levanta la mano y te muestra fijamente su palma abierta con los 5 dedos extendidos, no te preguntaras si te está saludando, sino que pensarás en el número 5, con independencia de que te esté mostrando 5 dedos.
Lo importante, pues, es el número, no la unidad de medida que expresa. Tanto da que tu amigo te muestre 5 dedos o 5 lápices, tú pensarás en el número 5.
Basándonos en este concepto, encontraremos otro importante juego numérico, asociado a las medidas enteras que definen el monumento: el lado de la base de 440 cr y la arista de 218 m. La pirámide tiene 4 lados y 4 aristas. El número que se obtiene de la suma de los 4 lados es 4 x 440 = 1.760; y el que resulta de la suma de las 4 aristas es 4 x 218 = 872. Y su diferencia es igual a 888.
Y el 888 es el número que contiene una de las claves secretas de la Gran Pirámide de Keops.
La ley matemática del número 888
Una vez reconstruido el modelo original de la Gran Pirámide y en vista de los resultados, devino imprescindible estudiar con detalle sus magnitudes: el perímetro, la superficie y el volumen.
A partir de la concepción abstracta del número que nos llega desde los pitagóricos, se consideraron las magnitudes de la Gran Pirámide como números, con independencia de la unidad de medida que designaban. Y ello dio como resultado una extraña ley asociada a un número singular: el 888.
En la adjunta Tabla de la Gran Pirámide (fig. 18) las magnitudes se hallan en codos reales y en metros. La investigación desarrollada permitió confirmar que la relación entre el codo real y el metro empleada en el monumento, fue 1 codo real = Φ2 / 5 metros, o lo que es lo mismo, 1 codo real = 2,61803399 / 5 metros = 0,52360680 metros.
Esta relación es, pues, la aplicada entre ambas unidades de medida, tanto en el perímetro de la Gran Pirámide, como en su superficie o en su volumen. Por tanto y como es lógico, para transformar codos reales en metros se multiplicó la medida en codos reales por 0,52360680; para hacerlo de cr2 a m2, se multiplicaron los cr2 dos veces por esa cifra, es decir, por su cuadrado; y para pasar de cr3 a m3 se multiplicaron los cr3 tres veces por la cifra antedicha, es decir, por su cubo.
FIGURA 18 LA GRAN PIRAMIDE Y EL ESPACIO
Figura 18. La Tabla de la Gran Pirámide, con sus magnitudes que cumplen la Ley del 888.
En la tabla adjunta (fig. 18) también se puede aplicar la teoría de conjuntos. Si ponemos sobre la mesa una cesta con 3 plátanos, 5 naranjas y 8 manzanas, podemos decir que en la cesta tenemos 16 frutas, porque estamos sumando elementos distintos de similar naturaleza.
Es por ello, que tanto si entendemos que las magnitudes son sólo números, como si aplicamos la teoría de conjuntos, podemos sumar codos reales o metros con independencia de que sean lineales, cuadrados o cúbicos. Y es por ello que también podemos sumar los números de las magnitudes obtenidas tal como se hallan en la última columna de la Tabla, donde se suman codos reales y metros.
La 1.ª columna suma 18.301.722. La 2.ª suma 2.671.509. Y la 3.ª suma 20.973.231. Separemos las cifras de 4 en 4, es decir, tomémoslas en unidades de 10.000.
En la 1.ª columna resultan 1.830 y 1.722. En la 2.ª obtenemos 267 y 1.509. Y en la 3.ª, 2.097 y 3.231. Sumemos los números de 2 en 2 y obtendremos, en todas ellas, múltiplos de 888:
1.830 + 1.722 = 3.552 = 888 x 4
267 + 1.509 = 1.776 = 888 x 2
2.097 + 3.231 = 5.328 = 888 x 6
A pesar de haber consultado a cualificados matemáticos, aún ninguno de ellos se ha podido explicar esta ley tan sorprendente. No sabemos cómo los sacerdotes-arquitectos egipcios pudieron establecerla. Y tampoco cómo pudieron llegar a construir la Gran Pirámide a partir de ella.
En el supuesto de que hoy conociéramos la Ley del 888 y, a partir de ella, intentásemos construir una pirámide que tuviera un perímetro, una superficie y un volumen prefijados, sólo podríamos hacerlo mediante sucesivas aproximaciones a través del ordenador. Quién sabe cuánto tiempo necesitaríamos para conseguirlo y si finalmente lo conseguiríamos o no.
Por tanto, la Ley del 888 presenta un doble enigma:
¿De dónde procedían los conocimientos matemáticos hallados en la Gran Pirámide?
¿Cómo consiguieron diseñar el monumento a partir de tener prefijados su perímetro, su superficie y su volumen por la Ley del 888?
Sin embargo, más allá de los enigmas, la Tabla de la Gran Pirámide nos aporta una importante certeza.
¡La Ley del 888 es la prueba irrefutable de que la reconstrucción del modelo original de la Gran Pirámide es totalmente exacta!
Y esta afirmación se basa en que dicha Ley no se cumpliría, si hubiera una desviación en el perímetro de la Gran Pirámide de un solo codo real sobre 8.388 cr, o de un solo codo real cuadrado en su superficie sobre 314.159 cr2, o de un solo codo real cúbico en su volumen sobre 17.979.175 cr3. Y en este último caso representaría que si la exactitud de la reconstrucción fuera de un 99,999994% no sería suficiente para que la Ley del 888 se cumpliese. Por tanto…
¡La Ley del 888 certifica la reconstrucción exacta del modelo de la Gran Pirámide en sus medidas originales!
Y la Ley del 888 también confirma que en la Gran Pirámide se usó una unidad de medida prácticamente igual a nuestro metro, que establecía la igualdad ya comentada entre 1 codo real y 0,523606797 metros.
[1] DORMION, Gilles – GOIDIN, Jean-Patrice. Kheops: Nouvelle Enquëte. Propositions Preliminaires. Editions Recherche sur les Civilisations. París, 1.986.
[2] Pitágoras nació en Samos en el siglo -VI.